Author: Gorenstein, Gryffindor, Class of 2024

前言

本文引入了组合统计量的概念，并探讨了其在序列上、格路径上的相关内容，并着重介绍了停车问题可解序列的集合 (Parking Function) 相关的定理及其与有标号有根森林 (Rooted labeled forests) 间的双射。

目录

  • 格路径的基本概念
    • 卡特兰数与 $\rm Dyck$ 路
      • 左右子树地位不等同的二叉树计数
    • $\rm Schröder$ 数
  • $\rm Parking$ 函数的基本概念
    • 判定
    • $\rm Parking$ 函数到 $\rm Dyck$ 路的映射
    • $\rm Parking$ 函数的计数
  • $q\text -$模拟与组合统计量
    • $q\text -$模拟
    • 排列上的组合统计量
  • 格路径的组合统计量
    • $\rm{q{-}Catalan}$ 数
    • 格路径与 $01$ 序列的对应
  • $\rm Parking$ 函数到树的双射
    • 有标号森林的基本概念
    • $\mathcal{PF}_n$ 与 $\mathcal F_n$ 的几个关联
    • 停车问题与树的双射
      • 映射 $\varphi:\mathcal {F_n}\to\mathcal{PF}_n$
      • 逆映射：$\varphi^{-1}:\mathcal{PF}_n\to\mathcal{F}_n$

格路径的基本概念

我们首先对格路径作一个基本介绍，作为后文与之相关内容的一个铺垫，并稍微探讨其计数问题。

卡特兰数与 Dyck 路

从 $(0,0)$ 走到 $(p,q)$ 的格路径为 $\binom{p+q}{p}=\binom{p+q}{q}$。现在考虑从 $(0,0)$ 至 $(p,q)$ 的下对角线格路径数量，我们可以将起点和终点各下移一格，将问题转化为求 $(0,-1)\to(p,q-1)$ 的总路径数量减去触碰或穿过对角线的路径数量。显然，这样的路径能与 $(-1,0)\to(p,q-1)$ 一一对应。

因之从 $(0,0)$ 至 $(p,q)$ 的不穿过对角线的格路径数量为：

\[\binom{p+q}{q}-\binom{p+1+q-1}{q-1}=\frac{p-q+1}{p+1}\binom{p+q}{q}\]

令 $p=q=n$，我们就得到了卡特兰数 $C$：

\[C_n=\frac{1}{n+1}\binom{2n}{n}\]

相仿地，一条不走到对角线下方的格路径称作 $\mathbf{Dyck}$ 路。所有 $n$ 阶 $\mathrm{Dyck}$ 路的集合记作 $\mathcal D_n$。

Delannoy 数

现在考虑不仅能水平、垂直前进，还可以沿右上对角线走一格（$\rm HVD$ 路径）时，从 $(0,0)$ 到 $(p,q)$ 的路径数。这个数就是 $\mathbf{Delannoy}$ 数。

如果使用了 $r$ 个对角步，那么剩下 $p-r,q-r$ 个垂直和水平步。设:

\[D(p,q:r)=\binom{p+q-r}{p-r\quad q-r\quad r}\]

则 $\rm Delannoy$ 数 $D(n,m)$ 为：

\[D(n,m)=\sum_{k=0}^{\min(n,m)}\binom{n+m-k}{n-k\quad m-k\quad k}=\sum_{k=0}^{\min(n,m)}\frac{(n+m-k)!}{(n-k)!(m-k)!k!}\]

递推关系

考虑 $C_n$ 的计数意义。我们枚举第一次碰到主对角线的 $k$，使 $(0,0)\to(k,k)$ 且中间不经过下对角线，即 $C_{k-1}$。而 $(k,k)\to(n,n)$ 就是 $C_{n-k}$。从而：

\[C_n=\sum_{k=1}^n C_{k-1}C_{n-k}=\sum_{k=0}^{n-1}C_{k}C_{n-k-1}\]

即：

\[C_{n+1}=\sum_{k=0}^nC_kC_{n-k}\]

设 $C(z)=\sum\limits_{k=0}^{\infty}C_kz^k$ 为卡特兰数列的生成函数，于是就有：

\[\begin{aligned} C^2(z)&=\sum_{s=0}^\infty\left(\sum_{k=0}^s C_kC_{s-k}\right)z^s=\sum_{k=0}^{\infty}C_{k+1}z^k\\& =\frac{1}{z}\sum_{k=0}^\infty C_{k+1}z^{k+1}=\frac{C(z)-1}{z} \end{aligned}\]

解出有意义的解为：

\[C(z)=\frac{1-\sqrt{1-4z}}{2z}\]

$C(z)$ 的展开

\[\begin{aligned} C(z)&=\frac{1-\sqrt{1-4z}}{2z}=\frac{1}{2z}\left(1-(1-4z)^\frac{1}{2}\right)\\ &=\frac{1}{2z}\left(1-\sum_{i=0}^{\infty}\binom{\frac{1}{2}}{i}(-4z)^i\right) \end{aligned}\]

从而：

\[\begin{aligned} C_n&=\left[z^n\right]C(z)=\frac{1}{2}\binom{\frac{1}{2}}{n+1}(-1)^n4^{n+1}\\ &=\frac{1}{2}\frac{\prod_{k=0}^n\left(\frac{1}{2}-k\right)}{(n+1)!}(-1)^n4^{n+1}\\ &=\frac{1}{2}\frac{\frac{1}{2}\prod_{k=1}^n\left(k-\frac{1}{2}\right)}{(n+1)!}4^{n+1}\\ &=\frac{1}{2}\frac{(2n)!}{2^nn!(n+1)!}2^{n+1}=\frac{(2n)!}{n!(n+1)!}\\ &=\frac{1}{n+1}\binom{2n}{n} \end{aligned}\]

左右子树地位不等同的二叉树计数

$\rm Catalan$ 数还出现在很多不同的场合，左右子树地位不等同的二叉树计数就是一个例子。

有两种方法可以得到其二叉树的生成函数。我们设 $\mathcal {A,B}$ 表可空和不可空的左右不等同二叉树组合类，那么有：

\[\mathcal A=\epsilon+\mathcal A{\times}{\circ}{\times}\mathcal A\] \[B=\circ+\mathcal B{\times}{\circ}+{\circ}{\times}\mathcal B+\mathcal B{\times}{\circ}{\times}\mathcal B\]

可解得：

\[A(z)=\frac{1-\sqrt{1-4z}}{2z},\quad B(z)=\frac{1-2z-\sqrt{1-4z}}{2z}\]

的确满足 $\mathcal A=\epsilon+\mathcal B$；这两种途径都得到了卡特兰数。事实上我们还可以代入其生成函数验证 $\mathcal A$ 和 $\mathcal B$ 的如下关系：

\[\mathcal A=\epsilon+\circ+\mathcal B{\times}{\circ}+{\circ}{\times}\mathcal B+\mathcal B{\times}{\circ}{\times}\mathcal B\]

Schröder 数

设 $(0,0)\to(p,q)$ 的下对角 $\rm HVD$ 路径的计数为 $R(p,q)$，并记 $R(p,q:r)$ 表示使用了 $r$ 个 $\rm D$ 移动的不穿过对角的路径。

除去 $r$ 个 $\rm D$ 路径后，剩下 $(p-r,q-r)$ 就是一个不穿过对角线上方的路径计数。然后将 $r$ 插入到 $\rm H,V$ 和两端的中间，总方案数为 $\binom{p+q-r}{r}$。简单计算可得：

\[R(n,m)=\sum_{k=0}^{\min(n,m)}R(n,m:k)\] \[=\sum_{k=0}^{\min(n,m)}\frac{n-m+1}{n-k+1}\frac{(n+m-k)!}{(n-k)!(m-k)!k!}\]

$\mathbf{ Schröder}$ 数 $R_n$ 定义为 $R(n,n)$：

\[R_n=\sum_{k=0}^n\frac{1}{n-k+1}\frac{(2n-k)!}{k!((n-k)!)^2}\]

所有 $n$ 阶 $\rm HVD$ 格路径的集合记作 $\mathcal S_n$。

生成函数

考虑从 $(0,0)\to (n,n)$ 的第一步。当这一步为 $(1,1)$ 时，此后的路径数目即为 $R_{n-1}$。而当第一步为 $(1,0)$ 时，我们总能找到一个 $1\leqslant k\leqslant n$ 的 $k$，使得 $k$ 是第一个碰到对角线的点。在 $k$ 前的路径个数是 $R_{k-1}$，$k$ 以后为 $R_{n-k}$。综合以上两类第一步的数量可得：

\[R_n=R_{n-1}+\sum_{k=1}^nR_{k-1}R_{n-k}=R_{n-1}+\sum_{k=0}^{n-1}R_kR_{n-1-k}\]

其中 $R_0=1$。从而：

\[z^nR_n=z\left(z^{n-1}R_{n-2}\right)+z\left(\sum_{k=0k}^{n-1}z^kR_{k}z^{n-1-k}R_{n-1-k}\right)\quad(n\geqslant 1)\]

令 $R(z)$ 为 $\rm Schröder$ 数的生成函数，因 $R_0=1$，故有：

\[R(z)=1+zR(z)+zR^2(z)\]

解出有意义的解为：

\[R(z)=\frac{1-z-\sqrt{z^2-6z+1}}{2z}\]

Parking 函数的基本概念

$n$ 元 $\mathbf{Parking}$ 函数 定义为一个使 $n$ 位停车问题可解的序列 $P=a_1a_2\dots a_n$。所有 $n$ 元 $\mathrm{Parking}$ 函数的集合记作 $\mathcal{PF}_n$。

停车问题

有 $n$ 个停车位和 $n$ 辆车，每辆车 $i$ 有一个偏好的停车位置 $a_i$。每辆车依次进入时，首先开到位置 $a_i$。若该位置有车，则在该车位沿往后最近的一个空位停车，求序列 $a_i$ 使得每辆车均可以停车成功。该问题称为停车问题。

判定

定理$\quad$序列 $a_1a_2a_3\dots a_n$ 是 $\rm Parking$ 函数，当且仅当 $a$ 重排后的序列 $b_1b_2\dots b_n$ 满足 $\forall i,b_i\leqslant i$。

$Proof.\quad$该判定等价于偏好 $1\sim i$ 的车大于等于 $i$ 辆。将 $n$ 个车位后面再加一个车位，并将 $n+1$ 个车位首尾接成一个环，则条件等价于位置 $n+1$ 无车停。

  • 充分性：假设满足该判定且位置 $n+1$ 有车，则必有一个 $i\leqslant n$ 无车。则此时偏好 $1\sim i$ 的车仅有 $i-1$ 辆，矛盾。
  • 必要性：位置 $n+1$ 无车，表明对于任意 $i\leqslant n$，位置 $1$ 至 $i$ 均停满车，即 $b_i\leqslant i$。

这就证明了该定理。$\square$

推论$\quad$一个 $\text{Parking}$ 函数的所有排列仍是 $\rm Parking$ 函数。

Parking 函数到 Dyck 路的映射

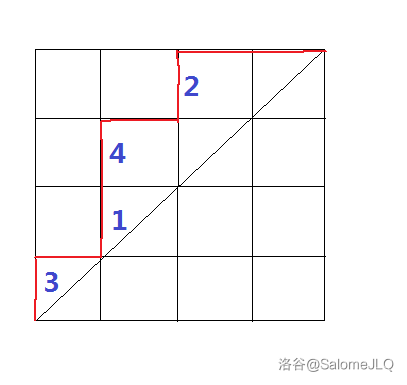
考虑一个 $\mathrm{Dyck}$ 路。将每辆汽车放在一个垂直步的正右一格位置，且限制若 $i$ 在 $j$ 的上方，则要求 $i>j$。

这样放置的意义为：若列 $i$ 上放置了车 $i_1,\dots,i_j$，则表明这些车以位置 $i$ 为最喜欢的车位。$\rm Parking$ 函数的要求暗含了 $\mathrm{Dyck}$ 路的要求，即，它满足了上述判定。

如果你不理解，请看下面这个例子。$4$ 辆车的偏好位置分别为 $a_1=2,a_2=3,a_3=1,a_4=2$，对应第一列上放置数字 $3$，第二列上放置数字 $1,4$，第三列上放置数字 $2$。$\rm Dyck$ 路不穿过主对角线的限制使这种放置满足了 $a$ 重排后 $b_i\leqslant i$ 的要求。

Parking 函数的计数

$n$ 元 $\rm Parking$ 函数的数量 $

\mathcal{P F}_n

$ 为：
\[(n+1)^{n-1}\]

$Proof.\quad$下面记 $[n]={1,2,\dots,n}$。考虑对上述环形停车问题稍作改变，即 $a_i\in[n+1]$。易见这个改变不影响成为 $\rm Parking$ 函数的条件，即，我们仍然需要对使得车位 $n+1$ 空出的序列进行计数。所有满足 $i\in[n],a_i\in[n+1]$ 的序列共有 $(n+1)^n$ 个，且每个序列必空出一个位置。由圆周的对称性，空出车位 $n+1$ 的数列数量，即 $n$ 元 $\rm Parking$ 函数的数量 $

\mathcal{PF}_n

$ 为 $(n+1)^{n-1}$。$\square$

$q\text -$模拟与组合统计量

一个组合统计量是一个组合类 $\mathcal A$ 到自然数集的具有组合意义的映射 $f:\mathcal A\to \mathbb{N}$。

$q\text -$模拟

一个非负整数 $n$ 的 $\mathbf q\text -$模拟 是一个关于 $q$ 的 $n-1$ 次多项式，记作 $[n]_q$，其为：

\[[n]_q=1+q+\dots+q^{n-1}\]

定义：

\[[n]!=[1]_q[2]_q\cdots[n]_q\,,\quad\begin{bmatrix}n\\k\end{bmatrix}_q=\frac{[n]!}{[k]![n-k]!}\]

为 $\mathbf{q}$-阶乘和 $\mathbf{q}$-二项式系数。显然 $\lim_{q\to1}\begin{bmatrix}n\k\end{bmatrix}_q(q)=\dbinom{n}{k}$。更一般地：

\[\begin{bmatrix}n\\m_1\quad m_2\quad \cdots\quad m_k\end{bmatrix}_q=\frac{[n]!}{[m_1]![m_2]!\cdots[m_k]!}\]

为 $\mathbf{q}$-多项式系数。

$q\text -$帕斯卡公式

\[\begin{bmatrix}n\\k\end{bmatrix}_q=q^{k-1}\begin{bmatrix}n-1\\k\end{bmatrix}_q+\begin{bmatrix}n-1\\k-1\end{bmatrix}_q\]

排列上的组合统计量

定理（Mahonian 性质）

定义 $\mathcal P_n$ 为 $[n]$ 上所有长度为 $n$ 的无重复序列的集合，设 $w\in\mathcal P_n$，定义组合统计量 $\operatorname{maj},\operatorname{inv}$ 为：

\[\operatorname{inv(w)}=\sum_{i<j,w_i>w_j}1\,,\quad\operatorname{maj(w)}=\sum_{w_i>w_{i+1}}i\]

则对于 $\rm maj,inv$，其具有 $\rm Mahonian$ 性质：

\[\sum_{\sigma\in \mathcal P_n}q^{\operatorname{inv(\sigma)}}=[n]!=\sum_{\sigma\in \mathcal P_n}q^{\operatorname{inv(\sigma)}}\]

$Proof.$

$\mathbf{inv}$ 部分$\quad$令 $h(\sigma)$ 为排列 $w$ 中在数 $n$ 右侧的数的个数，并记 $\sigma_1$ 为 $\sigma$ 去掉数 $n$ 后的结果，显然 $\sigma_1\in\mathcal P_{n-1}$，且有 $\operatorname{inv}(\sigma)=h(\sigma)+\operatorname{inv}(\sigma_1)$，故：

\[\begin{aligned} \sum_{\sigma\in\mathcal P_n}q^{\operatorname{inv(\sigma)}}&=\sum_{k=0}^{n-1}\sum_{\sigma\in \mathcal P_n,h(\sigma)=k}q^{\operatorname{inv}({\sigma})}=\sum_{k=0}^{n-1}\sum_{\sigma_1\in \mathcal P_{n-1}}q^{k+\operatorname{inv}(\sigma_1)}\\ &=\sum_{k=0}^{n-1}q^{k}\sum_{\sigma_1\in \mathcal P_{n-1}}q^{\operatorname{inv(\sigma_1)}}=[n]_q\sum_{_{\sigma\in \mathcal P_{n-1}}}q^{\operatorname{inv}(\sigma)}\end{aligned}\]

如是递归下去。显而易见 $\sum_{\sigma\in \mathcal P_1}q^{\operatorname{inv}({\sigma})}=[1]q$，立即证得 $\sum{\sigma\in \mathcal P_n}q^{\operatorname{inv(\sigma)}}=[n]_q[n-1]_q\cdots[1]_q=[n]!$。

$\mathbf{maj}$ 部分$\quad$当 $n$ 插入 $P_{n-1}$ 中任意 $\tau$ 的 $n$ 个间隔时，其增量恰取遍 $0,1,\dots,n-1$ 一次。从而：

\[\sum_{\sigma\in \mathcal P_n}q^{\operatorname{maj}(\sigma)}=\sum_{\tau\in \mathcal P_{n-1}}\sum_{k=0}^{n-1}q^{\operatorname{maj}(\tau)+k}=[n]\sum_{\tau\in \mathcal P_{n-1}}q^{\operatorname{maj}(\tau)}\]

边界与 $\rm inv$ 的情形是类似的，可得其为 $[n]!$。$\square$

一般地，如果组合统计量 $f$ 满足：

\[\sum_{\sigma\in \mathcal P_{n}}q^{f(\sigma)}=[n]!\]

则称这样的组合统计量 $f$ 为 $\mathbf{Mahonian}$ 的。

定理$\quad$设 $\mathbf{\alpha}=(m_1,m_2,\dots,m_k)\in\mathbb N^k,n=\sum_{\jmath}m_{\jmath}$，令 $\mathcal M_{\alpha}$ 表示其上所有全排列，则：

\[\sum_{w\in\mathcal M_{\alpha}}q^{\operatorname{inv}(w)}=\begin{bmatrix}n\\m_1\quad m_2\quad \cdots\quad m_k\end{bmatrix}_q=\sum_{w\in\mathcal M_{\alpha}}q^{\operatorname{maj}(w)}\]

格路径的组合统计量

Catalan 序列集与 Dyck 路集

一个序列被称之为 $\mathbf n$ 阶 $\mathbf{Catalan}$ 序列，如果其由 $n$ 个 $0$ 和 $n$ 个 $1$ 构成，且该序列的任一前缀中 $0$ 的个数均不小于 $1$ 的个数。所有 $n$ 阶 $\rm Catalan$ 序列构成的集合记作 $\mathcal{CW}_n$。

$\mathcal{CW}_n$ 和 $\mathcal D_n$ 间存在一个显然的双射：将 $0$ 与 $(0,1)$ 对应，将 $1$ 与 $(1,0)$ 对应。

q-Catalan 数

对于 $\mathcal D_n$ 中的一条 $\rm Dyck$ 路 $\Pi$，令 $a_i(\Pi)$ 为自下而上第 $i$ 行里 $\Pi$ 和主对角线之间的完整方格个数，并定义组合统计量 $\operatorname{area}$ ：

\[\operatorname{area}(\Pi)=\sum_{i=1}^n a_i(\Pi)\]

一个 $\mathbf{q-Catalan}$ 数 $C_n(q)$ 以如下形式定义：

\[C_n(q)\sum_{\Pi\in\mathcal D_n}q^{\operatorname{area}(\Pi)}\]

递推关系

定理$\quad$ 对任意正整数 $n$，有：

\[C_n(q)=\sum_{k=0}^n q^{k-1}C_{k-1}(q)C_{n-k}(q)\]

$Proof.\quad$令 $h(\Pi)$ 表示 $\Pi$ 从 $(0,0)$ 以后第一次碰到主对角线时的高度，则点 $(h(\Pi),h(\Pi))$ 将 $\Pi$ 分为 $\Pi_1,\Pi_2$ 上下两段。设 $k=h(\Pi)$，显然 $\Pi_1$ 必经过 $(0,1),(k-1,k)$ 两点。设该 $(0,1)$ 至 $(k-1,k)$ 段路径为 $\Pi_3$。于是 $1\leqslant k\leqslant n$，且 $\Pi_1\in\mathcal D_k,\Pi_2\in\mathcal D_{n-k},\Pi_3\in\mathcal D_{k-1}$，且：

\[\operatorname{area}(\Pi)=\operatorname{area}(\Pi_1)+\operatorname{area}(\Pi_2)=k-1+\operatorname{area}(\Pi_3)+\operatorname{area}(\Pi_2)\]

则：

\[\begin{aligned} C_n(q)&=\sum_{k=1}^n\sum_{\Pi\in\mathcal D_n,h(\Pi)=k}q^{\operatorname{area}(\Pi)}\\ &=\sum_{k=1}^n q^k\left(\sum_{\Pi_3\in\mathcal D_{k-1}}q^{\operatorname{area}(\Pi_3)}\times \sum_{\Pi_2\in\mathcal D_{k}}q^{\operatorname{area}(\Pi_2)}\right)\\ &=\sum_{k=0}^n q^{k-1}C_{k-1}(q)C_{n-k}(q)\end{aligned}\]

另一个定理

\[\sum_{w\in\mathcal{CW_n}}q^{\operatorname{maj}(w)}=\frac{1}{[n+1]_q}\begin{bmatrix}2n\\n\end{bmatrix}_q\]

格路径与 01 序列的对应

一条从 $(0,0)$ 到 $(m,n)$ 的只由 $(0,1),(1,0)$ 步构成的路径称之为 $\mathbf{(m,n)}$ 格路径。所有 $(m,n)$ 格路径的集合记作 $\mathcal L_{m,n}$。

记全体 $m$ 个 $1$，$n$ 个 $0$ 的 0/1 序列集合为 $\mathcal M_{m,n}$。$\mathcal L_{m,n}$ 到 $\mathcal M_{m,n}$ 有一个显然的双射：将 $0$ 与 $(0,1)$ 对应，将 $1$ 与 $(1,0)$ 对应。

设 $L\in \mathcal L_{m,n}$，令 $a_i(L)$ 为第 $i$ 行与纵坐标轴 $x=0$ 之间的方格数，定义：

\[\operatorname{area}(L)=\sum_{i=1}^n a_i(L)\]

定理$\quad$设 $L\in \mathcal L_{m,n}$ 与 $w_{L}\in \mathcal M_{m,n}$ 是上述双射对应的一对元素，则：

\[\operatorname{area}(L)=\operatorname{inv}(w_{L})\]

推论

\[\sum_{L\in\mathcal L_{m,n}}q^{\operatorname{area}(L)}=\begin{bmatrix}m+n\\n\end{bmatrix}_q\]

Parking 函数到树的双射

这是本文讨论的最后一个话题，也是本文介绍的主要对象之一。作为本文的最后一部分，我们将讨论经典的停车问题与标记树的联系，并给出一个双射。

有标号森林的基本概念

一个由有标号树构成的森林称之为有标号森林，特别地，有标号有根树构成的森林称为有标号有根森林 (Rooted Labeled Forests)。记所有由 $n$ 个点构成的有标号有根森林集合为 $\mathcal F_n$。

$n$ 个点的有标号有根森林数量就是 $n+1$ 个点的标记树数量，因此有：

\[\left|\mathcal F\_n\right|=\(n+1)^{n-1}\]

这个等式可以用矩阵树定理证明，这在我们的讨论范围以外。

有标号有根森林的组合统计量

定义：

\[\operatorname{inv}(F;v)=\operatorname{card}\big(\{(v,u)\mid u\in\operatorname{des}(v),u<v\}\big)\]

其中 $\operatorname{des}(v)=\operatorname{subtree}(v)\setminus{v}$，即 $v$ 的子树除去 $v$ 以外的点构成的集合 (descendant)，并定义组合统计量 $\operatorname{inv}(F)$：

\[\operatorname{inv}(F)=\sum_{v}\operatorname{inv} (F;v)\]

称一个节点 $v$ 是一个 leader，如果 $\operatorname{inv}(F;v)=0$。定义组合统计量 $\operatorname{lead}(F)$：

\[\operatorname{lead}(F)=\operatorname{card}\big(\{v\mid v\text{ is a leader in }F\}\big)\]

$\mathcal{PF_n}$ 与 $\mathcal F_n$ 的几个关联

定理$\quad n$ 元 $\rm Parking$ 函数的数量和 $n$ 个点的有标号森林数量相等，即：

\[|\mathcal{PF\_n}|=\(n+1)^{n-1}=|\mathcal F\_n|\]

这启示我们可能存在某些双射。该式的两端在上文均已解释。

Parking 函数的组合统计量

设 $P=p_1p_2\dots p_n,P\in\mathcal{PF}_n$，$P$ 中每辆车最终停车位置为 $q_1,q_2,\dots,q_n$，令 $\operatorname{jump}(P;i)=p_i-q_i$，并令组合统计量 $\operatorname{jump}(P)$ 为：

\(\operatorname{jump}(P)=\sum_{i=1}^n \operatorname{jump}(P;i)\) 注意到：

\[\begin{aligned} \operatorname{jump}(P)&=(q_1+q_2+\dots+q_n)-(p_1+p_2+\dots+p_n)\\ &=\binom{n+1}{2}-\sum_{\jmath} p_{\jmath} \end{aligned}\]

对于 $P$ 的一个 $c$，称其为 lucky 的，如果 $ \operatorname{jump}(P;c)=0$，即，它恰好停到了偏好的位置。定义组合统计量 $ \operatorname{lucky}(P)$：

\[\operatorname{lucky}(F)=\operatorname{card}\big(\{c\mid c\text{ is lucky}\}\big)\]

组合统计量上的联系

注意到：

\[\begin{aligned} \sum_{F\in\mathcal{F}_1}q^{\operatorname{inv}(F)}&=1\\ \sum_{F\in\mathcal{F}_2}q^{\operatorname{inv}(F)}&=2+q\\ \sum_{F\in\mathcal{F}_3}q^{\operatorname{inv}(F)}&=6+6q+3q^2+q^3 \end{aligned}\] \[\begin{aligned} \sum_{P\in\mathcal{PF}_1}q^{\operatorname{jump}(P)}&=1\\ \sum_{P\in\mathcal{PF}_2}q^{\operatorname{jump}(P)}&=2+q\\ \sum_{P\in\mathcal{PF}_3}q^{\operatorname{jump}(P)}&=6+6q+3q^2+q^3 \end{aligned}\]

事实上，这的确是一个一般的规律。我们有：

  1. 定理 (G.Kreweras 1980)
\[\sum\_{F\in\mathcal{F}\_n}q^{\operatorname{inv}\(F)}=\sum\_{P\in\mathcal{PF}\_n}q^{\binom{n+1}{2}-|P|}\]
  1. 定理 (Gessel-Seo 2004)
\[\sum_{F\in\mathcal F_n}u^{\operatorname{lead}(F)}=u\prod_{i=1}^{n-1}(i+(n-i+1)u)=\sum_{P\in\mathcal{PF}_n}u^{\operatorname{lucky}(P)}\]
  1. 定理 (S. 2008)
\[\sum_{F\in\mathcal F_n}q^{\operatorname{inv}(F)}u^{\operatorname{lead}(F)}=\sum_{P\in\mathcal{PF}_n}q^{\operatorname{jump}(P)}u^{\operatorname{lucky}(P)}\]

至此，我们可以进入本文最终的部分。

停车问题与树的双射

映射 $\varphi:\mathcal {F_n}\to\mathcal{PF}_n$

考虑任意一个 $n$ 有标号有根森林 $F$。新增一个节点 $n+1$，并将所有根向节点 $n+1$ 连边，形成一棵以 $n+1$ 为根的标记树，记作树 $T$。借用一张里昂大学的一篇课件上的图：

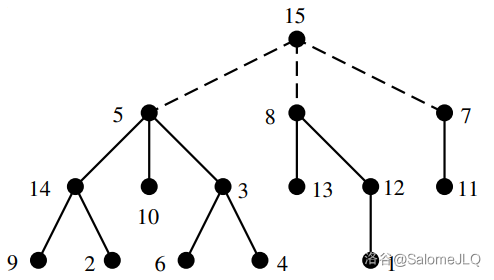
现在，我们对这棵树的每一个节点 $x$ 的子树进行如下操作：

  • 取出 $x$ 后代中标号大于 $x$ 的节点；
  • 保序地重排这些节点，即将取出的节点从小到大排名为 $a_1,a_2,\dots,a_m$，令 $a_i(i<m)$ 移动到原先 $a_{i+1}$ 的位置；
  • 将 $x$ 移动到 $a_1$ 的位置，将 $a_m$ 移动到 $x$ 的位置。

易见点的操作顺序不影响结果，且操作后形成的树唯一。对每一个 $x$ 都如是操作后，我们将得到一棵对于任意节点（不妨设其标号为 $x$）都有 $x$ 大于其任意后代标号的树。我们将这棵新树记作 $D$。

但是有多棵树都有可能重排出树 $D$。为此，我们引入：

  • 树 $I$：与树 $T$ 结构相同，其每个点的点权为树 $T$ 中该点的 $\mathrm{inv}$。
  • 树 $C$：与树 $T$ 结构相同，其每个点的点权为对其后根遍历所得的次序。

将树 $D,C,I$ 结合，构成树 $D\times(C-I)$，即：每个点有一个标号 $x$ 和一个点权 $v(x)$，其中 $x$ 即为树 $D$ 中的 $x$，$v(x)$ 为树 $C$ 中该点的点权减去树 $I$ 中该点的点权。

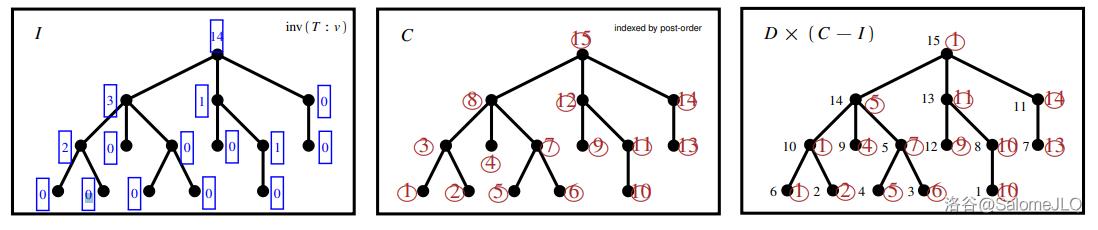
由此，我们可以还原出树 $T$。并且，我们已经得到了 $\mathcal F_n\to\mathcal{PF}_n$ 的一个单射：按标号依序取出每个点 $x$，则 $v(x)$ 即为车 $x$ 的偏好停车位置。例如在上图中，这个 $\rm Parking$ 函数 $P$ 为：

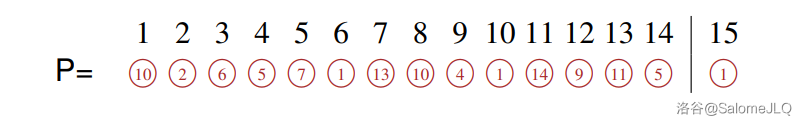
逆映射：$\varphi^{-1}:\mathcal{PF}_n\to\mathcal{F}_n$

考虑任意一个 $\rm Parking$ 函数 $P$。这里以上文出现过的例子为例：

\[P=\text{ 10\; 2\; 6\; 5\; 7\; 1\; 13\; 10\; 4\; 1\; 14\; 9\; 11 }\]

该 $\rm Parking$ 函数给出了一个最终的停车序列。在上例中：

\[\begin{aligned} \mathrm{Parking\;Space}&=1\;\;2\;\;3\;\;\;\,4\;\;5\;\;6\;\;7\;\;\,8\;\;\;\,9\;\;\;\,10\;\;11\;\;12\;\;13\;\ 14\quad\,\,\,15\\ \mathrm{Car's\;Number\;}c&=6\;\;2\;\;10\;\;9\;\;4\;\;3\;\;5\;\;14\;\;12\;\;1\;\;\;\,8\;\;\;\;13\;\;\,7\;\;\ \,11\quad\ \,15\\ \mathrm{jump}(P;c)&=0\;\;0\;\;2\;\;\;\,0\;\;0\;\;0\;\;0\;\;3\;\;\;\;0\;\;\;\,0\;\;\;\;1\;\;\;\,1\;\;\;\;\,0\;\;\;\,0\quad\ \ \,\,14 \end{aligned}\]

现在，对于每一个停车位 $x$，设其上停的车为 $c(x)$，则将 $x$ 向其后第一个 $c(y)>c(x)$ 的停车位 $y$ 连边。

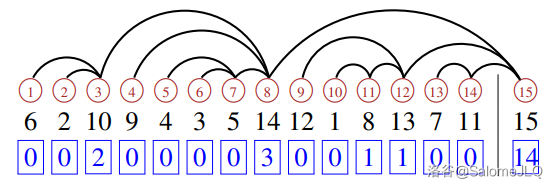
我们就获得了树 $T,C$ 和 $I$。易见其是唯一的，且任意一个 $\rm Parking$ 函数 $P\in\mathcal{PF}_n$ 都能如是构建出相应的树。这样，我们就完成了 $\varphi^{-1}:\mathcal{PF}_n\to\mathcal F_n$。

至此，我们解释了 $\mathcal{PF}_n$ 与 $\mathcal F_n$ 的集合大小相等的原因，并对其组合统计量间的联系给出了一个直观的表示。

参考文献：

  1. 组合数学 / 冯荣权，宋春伟编著。北京大学出版社，2015.8
  2. Forests and Parking Functions , Heesung Shin, Institut Camille Jordan, Université Claude Bernard Lyon-I, France. (THE 61ST SÉMINAIRE LOTHARINGIEN DE COMBINATOIRE. CURIA, PORTUGAL, SEP. 24, 2008)